Checking Sign Conventions

The sign convention for current varies between sources of battery data. Some define “charging” as positive whereas for others charging is negative current. The SignConventionChecker class checks whether our sign choice in the battery-data-toolkit, “charging current is postive,” is followed.

%matplotlib inline
from matplotlib import pyplot as plt
from battdat.consistency.current import SignConventionChecker
from battdat.data import CellDataset
from datetime import datetime, timedelta

Load Example Data

We have two simple cells that vary only by the where the “cycle” starts.

from battdat.io.batterydata import BDReader
dataset = BDReader().read_dataset(['../../../tests/files/batterydata/p492-13-raw.csv'])

Voltage Should Increase During Charge

The core concept behind our sign convention is that the voltage for a battery should increase while it is charging: an principle that is true for many types of batteries.

The algorithm for checking a dataset is consistent with this principle is conceptually simple: 1. Find a point where the current is the most constant 2. Measure the slope between voltage and time. 3. Make sure the slope and the current have the same sign (if voltage 📈, current ➕)

There are, however, a few nuances to the actual implementation.

Step 1: Finding a Region of Stable Current

Time spans with stable current are where the standard deviation of current is small. The checker finds the most-stable region using Panda’s windowing function.

Start by converting the “test_time” column in data to a Python time object so that Pandas can compute windows corresponding to a specific time span.

raw_data = dataset.raw_data.query('test_time < 8000').copy()  # Get a subset of the timesteries
raw_data['timestamp'] = raw_data['test_time'].apply(datetime.fromtimestamp)

A window of 6 minutes is short enough to find nearly-constant spans of current and long enough that transient fluctuations in voltage should have a minimal expect. > NOTE: The window size is an adjustable parameter in SignConventionChecker

current_std = raw_data.rolling(timedelta(seconds=360), on='timestamp')['current'].std()

fig, ax = plt.subplots(figsize=(3., 1.8))

ax.plot(raw_data['test_time'], raw_data['current'], label='$I$ (A)')
ax.plot(raw_data['test_time'], current_std, label='$\\sigma_I$ (A)')

ax.legend()
ax.set_xlabel('Time (s)')

Text(0.5, 0, 'Time (s)')

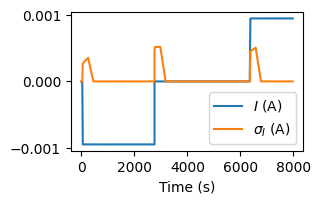
There are plenty of regions of stable current in this data and some where the current is nonzero.

window = raw_data.query('1000 < test_time < 2000')

window

	cycle_number	step_index	test_time	current	voltage	temperature	time	timestamp
16	0	5	1052.958	-0.00095	3.183413	29.8454	1.578067e+09	1969-12-31 19:17:32.958
17	0	5	1252.962	-0.00095	3.166171	29.8776	1.578067e+09	1969-12-31 19:20:52.962
18	0	5	1452.960	-0.00095	3.148165	29.8937	1.578067e+09	1969-12-31 19:24:12.960
19	0	5	1652.958	-0.00095	3.129091	29.8454	1.578067e+09	1969-12-31 19:27:32.958
20	0	5	1852.962	-0.00095	3.109255	29.8293	1.578068e+09	1969-12-31 19:30:52.962

Step 2: Compute the slope between voltage and time

The slope between two variables is proportional to the covariance, which can also be computed for a rolling window

cov = raw_data.rolling(timedelta(seconds=360), on='timestamp')['voltage'].cov(raw_data['test_time'])

fig, axs = plt.subplots(3, 1, figsize=(3., 2.4), sharex=True)

axs[0].plot(raw_data['test_time'], raw_data['voltage'])
axs[0].set_ylabel('$V$ (V)')

axs[1].plot(raw_data['test_time'], raw_data['current'] * 1000)
axs[1].set_ylabel('$I$ (mA)')

axs[2].plot(raw_data['test_time'], cov)
axs[2].set_ylabel('$\\sigma_{V,t}$ (mA)')

ax.legend()
ax.set_xlabel('Time (s)')

Text(0.5, 24.0, 'Time (s)')

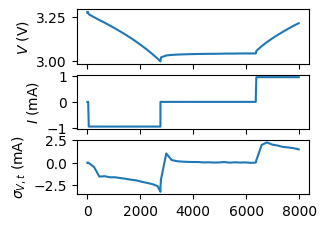
Note how the covariance between voltage and time (\(\sigma_{V,t}\)) has the same sign as the current for the regions where the data are the same.

Step 3: Compare signs

The SignConventionChecker does these two previous steps and compares the outcome

chckr = SignConventionChecker()
chckr.check(dataset)

[]

No errors for this dataset. ✅

If we change the sign, the checker will notice and report why the data are wrong

dataset.raw_data['current'] *= -1
chckr.check(dataset)

['Potential sign error in current. Average current between test_time=299170.4s and test_time=299530.4 is 9.5e-03 A and the covariance between the voltage and current is -1.5e+00 V-s. The current and this covariance should have the same sign.']