Defining Complex Charge Dependence in ECMs

Many parameters in equivalent circuit models (ECMs) depend on how charged the battery is. The most common example is that the voltage of a cell increases with the state of charge (SOC). Moirae provides several routes to expressing the SOC dependence for different properties

Interpolated SOC Dependence

Define a complex dependence on SOC using SOCInterpolatedHealth

from moirae.models.components.soc import SOCInterpolatedHealth
from moirae.models.ecm.utils import realistic_fake_ocv
import numpy as np

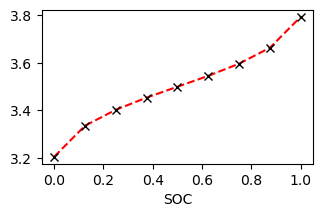
This function takes the values of the property at specific states of charge.

soc = np.linspace(0, 1, 9)
points = realistic_fake_ocv(soc)

Supply both the value of the function (base_values) and, optionally, the points at which they are evaluated.

Moirae assumes evenly-spaced SOC points between 0 and 1 by default.

ocv = SOCInterpolatedHealth(
    base_values=points,
    soc_pinpoints=soc,
    interpolation_style='linear',
)

%matplotlib inline
from matplotlib import pyplot as plt
fig, ax = plt.subplots(figsize=(3.5, 2.))

# Evaluate the function
#  Always returns a 2D array. First is the batch size, last is the property
value = ocv.get_value(soc)[0, :]
ax.plot(soc, value, 'r--')
ax.plot(soc, points, 'kx')

ax.set_xlabel('SOC')

Text(0.5, 0, 'SOC')

Interpolation with Polynomial Scaling

Interpolation functions can capture complex function shapes, at the expense of many fitting parameters.

The ScaledSOCInterpolatedHealth keep can keep the complex shapes of interpolated functions and instead a few “scaling” parameters that describe small changes to the shape.

Use the ScaledSOCInterpolatedHealth to define SOC dependence in two layers:

• base_values, soc_points: The base shape of the functional dependence

• scaling_coeffs: Parameters of a Legendre polynomial used to adjust the shape.

Aside: Legendre Polynomials are good for interpolation because each polynomial is orthogonal to all others)

from moirae.models.components.soc import ScaledSOCInterpolatedHealth

The interpolated curve is unchanged if all scaling parameters are zero. The first parameter introduces the same change to all points, the second adds a linear dependence to SOC, the third a quadratic, and so on.

ocv = ScaledSOCInterpolatedHealth(
    base_values=points,
    scaling_coeffs=[0., 0., 0.]
)

Evaluate with a few changes

scaled_allzero = ocv.get_value(soc)[0, :]

ocv.scaling_coeffs[0, 0] = 0.05
scaled_constant = ocv.get_value(soc)[0, :]

ocv.scaling_coeffs[0, :2] = [0., 0.1]
scaled_linear = ocv.get_value(soc)[0, :]

ocv.scaling_coeffs[0, 1:] = [0, 0.1]
scaled_quadra = ocv.get_value(soc)[0, :]

fig, ax = plt.subplots(figsize=(3.5, 2.))

# Evaluate the function
#  Always returns a 3D array. First two are batch sizes, last is the property
ax.plot(soc, value, 'k--', label='Intepolated')
ax.plot(soc, scaled_allzero, 'r', label='No Scaling', alpha=0.5)
ax.plot(soc, scaled_constant, 'b', label='Constant', alpha=0.5)
ax.plot(soc, scaled_linear, color='purple', label='Linear', alpha=0.5)
ax.plot(soc, scaled_quadra, color='orange', label='Quadratic', alpha=0.5)

ax.legend(fontsize=8)
ax.set_xlabel('SOC')

Text(0.5, 0, 'SOC')

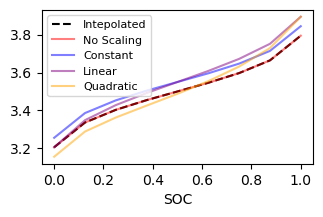
Estimators could adjust the slightly by fitting 3 ocv.scaling_coeffs instead of fitting all 9 ocv.base_values points.

Polynomial Dependence

Define a simpler function as a polynomials. At present, we only support Power Series polynomials but open an Issue if you’d like another type (see NumPy’s list).

from moirae.models.components.soc import SOCPolynomialHealth

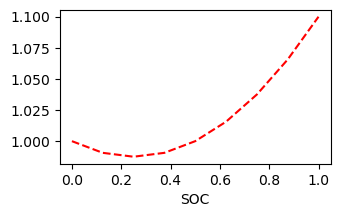
Define the polynomial using

r0 = SOCPolynomialHealth(
    coeffs=[1, -0.1, 0.2]  # 1 - 0.1 x + 0.2 x ^ 2
)

fig, ax = plt.subplots(figsize=(3.5, 2.))

# Evaluate the function
#  Always returns a 2D array. First is the batch size, last is the property
value = r0.get_value(soc)[0, :]
ax.plot(soc, value, 'r--')

ax.set_xlabel('SOC')

Text(0.5, 0, 'SOC')

Advanced: Batching and SOC Dependence

Moirae estimators guess batches of parameter values that may include both multiple values for interpolation points and multiple values of SOC.

The output if therefore two “batch size” x “number of SOC values per batch”

help(ocv.get_value)

Help on method get_value in module moirae.models.components.soc:

get_value(soc: Union[numbers.Number, List[float], numpy.ndarray], batch_id: int | None = None) -> numpy.ndarray method of moirae.models.components.soc.ScaledSOCInterpolatedHealth instance
    Computes value(s) at given SOC(s).

    Args:
        soc: Values at which to compute the property. Dimensions must be either

            1. a 2D array of shape `(batch_size, soc_dim)`. The `batch_size` must either be 1 or
               equal to the batch size fo the parameters.
            2. a 1D array of shape `(soc_dim,)`, in which case we will consider the `batch_size` to be equal to 1
            3. a 0D array (a scalar), in which case both `batch_size` and `soc_dim` are equal to 1.
        batch_id: Which batch member for the parameters and input SOC values to use. Default is to use whole batch
    Returns:
        Interpolated values as a 2D with dimensions (batch_size, soc_points).
        The ``batch_size`` is 0 when ``batch_id`` is not None.

Provide multiple guesses for scaling points will affect the first point.

ocv.scaling_coeffs = np.array([[0., 0.], [0.01, 0.01]])

outputs = ocv.get_value(soc)
outputs.shape

(2, 9)

The array is 2 (batch size of parameter functions) x 9 (number of SOC points in the evaluation)

fig, ax = plt.subplots(figsize=(3.5, 2))

for i, y in enumerate(outputs[:, :]):
    ax.plot(soc, y, label=f'Guess #{i}')

ax.legend(fontsize=8)
ax.set_xlabel('SOC')

Text(0.5, 0, 'SOC')

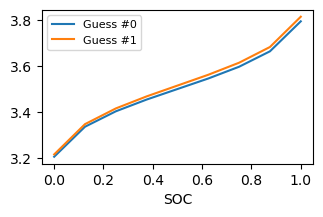
Each member of the output batch is with a different value of parameters

It is also possible to save execution time by only evaluating a single row of a batch

outputs = ocv.get_value(soc, batch_id=0)
outputs.shape

(1, 9)